Regression with Tensorflow/Keras

rpi.analyticsdojo.com

81. Regression with Tensorflow/Keras

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib

import matplotlib.pyplot as plt
from scipy.stats import skew
from scipy.stats.stats import pearsonr


%config InlineBackend.figure_format = 'retina' #set 'png' here when working on notebook
%matplotlib inline

!wget https://raw.githubusercontent.com/rpi-techfundamentals/spring2019-materials/master/input/boston_test.csv && wget https://raw.githubusercontent.com/rpi-techfundamentals/spring2019-materials/master/input/boston_train.csv

--2021-12-06 17:33:39--  https://raw.githubusercontent.com/rpi-techfundamentals/spring2019-materials/master/input/boston_test.csv
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 185.199.111.133, 185.199.109.133, 185.199.110.133, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|185.199.111.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 451405 (441K) [text/plain]
Saving to: ‘boston_test.csv’


boston_test.csv       0%[                    ]       0  --.-KB/s               
boston_test.csv     100%[===================>] 440.83K  --.-KB/s    in 0.02s   

2021-12-06 17:33:39 (20.1 MB/s) - ‘boston_test.csv’ saved [451405/451405]

--2021-12-06 17:33:39--  https://raw.githubusercontent.com/rpi-techfundamentals/spring2019-materials/master/input/boston_train.csv
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 185.199.108.133, 185.199.111.133, 185.199.109.133, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|185.199.108.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 460676 (450K) [text/plain]
Saving to: ‘boston_train.csv’

boston_train.csv    100%[===================>] 449.88K  --.-KB/s    in 0.03s   

2021-12-06 17:33:40 (13.1 MB/s) - ‘boston_train.csv’ saved [460676/460676]

train = pd.read_csv("boston_train.csv")
test = pd.read_csv("boston_test.csv")

train.head()

	Id	MSSubClass	MSZoning	LotFrontage	LotArea	Street	Alley	LotShape	LandContour	Utilities	LotConfig	LandSlope	Neighborhood	Condition1	Condition2	BldgType	HouseStyle	OverallQual	OverallCond	YearBuilt	YearRemodAdd	RoofStyle	RoofMatl	Exterior1st	Exterior2nd	MasVnrType	MasVnrArea	ExterQual	ExterCond	Foundation	BsmtQual	BsmtCond	BsmtExposure	BsmtFinType1	BsmtFinSF1	BsmtFinType2	BsmtFinSF2	BsmtUnfSF	TotalBsmtSF	Heating	...	CentralAir	Electrical	1stFlrSF	2ndFlrSF	LowQualFinSF	GrLivArea	BsmtFullBath	BsmtHalfBath	FullBath	HalfBath	BedroomAbvGr	KitchenAbvGr	KitchenQual	TotRmsAbvGrd	Functional	Fireplaces	FireplaceQu	GarageType	GarageYrBlt	GarageFinish	GarageCars	GarageArea	GarageQual	GarageCond	PavedDrive	WoodDeckSF	OpenPorchSF	EnclosedPorch	3SsnPorch	ScreenPorch	PoolArea	PoolQC	Fence	MiscFeature	MiscVal	MoSold	YrSold	SaleType	SaleCondition	SalePrice
0	1	60	RL	65.0	8450	Pave	NaN	Reg	Lvl	AllPub	Inside	Gtl	CollgCr	Norm	Norm	1Fam	2Story	7	5	2003	2003	Gable	CompShg	VinylSd	VinylSd	BrkFace	196.0	Gd	TA	PConc	Gd	TA	No	GLQ	706	Unf	0	150	856	GasA	...	Y	SBrkr	856	854	0	1710	1	0	2	1	3	1	Gd	8	Typ	0	NaN	Attchd	2003.0	RFn	2	548	TA	TA	Y	0	61	0	0	0	0	NaN	NaN	NaN	0	2	2008	WD	Normal	208500
1	2	20	RL	80.0	9600	Pave	NaN	Reg	Lvl	AllPub	FR2	Gtl	Veenker	Feedr	Norm	1Fam	1Story	6	8	1976	1976	Gable	CompShg	MetalSd	MetalSd	None	0.0	TA	TA	CBlock	Gd	TA	Gd	ALQ	978	Unf	0	284	1262	GasA	...	Y	SBrkr	1262	0	0	1262	0	1	2	0	3	1	TA	6	Typ	1	TA	Attchd	1976.0	RFn	2	460	TA	TA	Y	298	0	0	0	0	0	NaN	NaN	NaN	0	5	2007	WD	Normal	181500
2	3	60	RL	68.0	11250	Pave	NaN	IR1	Lvl	AllPub	Inside	Gtl	CollgCr	Norm	Norm	1Fam	2Story	7	5	2001	2002	Gable	CompShg	VinylSd	VinylSd	BrkFace	162.0	Gd	TA	PConc	Gd	TA	Mn	GLQ	486	Unf	0	434	920	GasA	...	Y	SBrkr	920	866	0	1786	1	0	2	1	3	1	Gd	6	Typ	1	TA	Attchd	2001.0	RFn	2	608	TA	TA	Y	0	42	0	0	0	0	NaN	NaN	NaN	0	9	2008	WD	Normal	223500
3	4	70	RL	60.0	9550	Pave	NaN	IR1	Lvl	AllPub	Corner	Gtl	Crawfor	Norm	Norm	1Fam	2Story	7	5	1915	1970	Gable	CompShg	Wd Sdng	Wd Shng	None	0.0	TA	TA	BrkTil	TA	Gd	No	ALQ	216	Unf	0	540	756	GasA	...	Y	SBrkr	961	756	0	1717	1	0	1	0	3	1	Gd	7	Typ	1	Gd	Detchd	1998.0	Unf	3	642	TA	TA	Y	0	35	272	0	0	0	NaN	NaN	NaN	0	2	2006	WD	Abnorml	140000
4	5	60	RL	84.0	14260	Pave	NaN	IR1	Lvl	AllPub	FR2	Gtl	NoRidge	Norm	Norm	1Fam	2Story	8	5	2000	2000	Gable	CompShg	VinylSd	VinylSd	BrkFace	350.0	Gd	TA	PConc	Gd	TA	Av	GLQ	655	Unf	0	490	1145	GasA	...	Y	SBrkr	1145	1053	0	2198	1	0	2	1	4	1	Gd	9	Typ	1	TA	Attchd	2000.0	RFn	3	836	TA	TA	Y	192	84	0	0	0	0	NaN	NaN	NaN	0	12	2008	WD	Normal	250000

5 rows × 81 columns

all_data = pd.concat((train.loc[:,'MSSubClass':'SaleCondition'],
                      test.loc[:,'MSSubClass':'SaleCondition']))

81.1. Data preprocessing:

We’re not going to do anything fancy here:

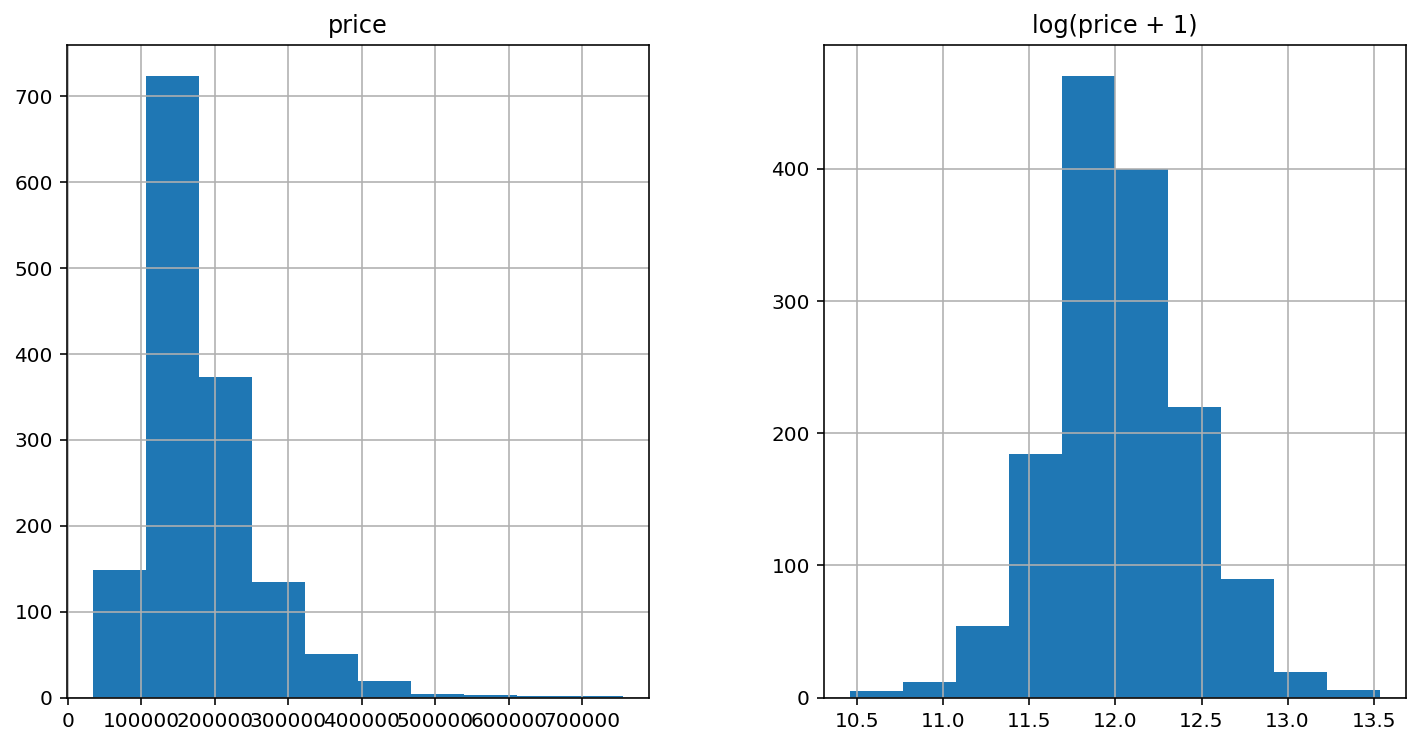
• First I’ll transform the skewed numeric features by taking log(feature + 1) - this will make the features more normal

• Create Dummy variables for the categorical features

• Replace the numeric missing values (NaN’s) with the mean of their respective columns

matplotlib.rcParams['figure.figsize'] = (12.0, 6.0)
prices = pd.DataFrame({"price":train["SalePrice"], "log(price + 1)":np.log1p(train["SalePrice"])})
prices.hist()

array([[<matplotlib.axes._subplots.AxesSubplot object at 0x7f909483f050>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x7f909399b910>]],
      dtype=object)

#log transform the target:
train["SalePrice"] = np.log1p(train["SalePrice"])

#log transform skewed numeric features:
numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index

skewed_feats = train[numeric_feats].apply(lambda x: skew(x.dropna())) #compute skewness
skewed_feats = skewed_feats[skewed_feats > 0.75]
skewed_feats = skewed_feats.index

all_data[skewed_feats] = np.log1p(all_data[skewed_feats])

all_data = pd.get_dummies(all_data)

#filling NA's with the mean of the column:
all_data = all_data.fillna(all_data.mean())

#creating matrices for sklearn:
X_train = all_data[:train.shape[0]]
X_test = all_data[train.shape[0]:]
y_train = train.SalePrice

81.2. Models Deep Learning Models

Now we are going to use Deep Learning models

from keras.models import Sequential
from keras.layers import Dense
from keras import metrics
import tensorflow as tf

#Create our model using sequential mode
model = Sequential()
model.add(tf.keras.layers.Normalization(axis=-1))
model.add(Dense(units=1))
model.compile(
    optimizer=tf.optimizers.Adam(learning_rate=0.1),
    loss='mean_absolute_error')

model.fit( X_train, y_train, epochs=100, verbose=2, validation_split = 0.2)
model.summary()

Epoch 1/100
37/37 - 1s - loss: 235.2399 - val_loss: 31.6727 - 851ms/epoch - 23ms/step
Epoch 2/100
37/37 - 0s - loss: 83.1837 - val_loss: 155.9600 - 75ms/epoch - 2ms/step
Epoch 3/100
37/37 - 0s - loss: 73.9159 - val_loss: 113.8599 - 67ms/epoch - 2ms/step
Epoch 4/100
37/37 - 0s - loss: 83.4473 - val_loss: 70.3255 - 67ms/epoch - 2ms/step
Epoch 5/100
37/37 - 0s - loss: 82.2961 - val_loss: 82.0233 - 69ms/epoch - 2ms/step
Epoch 6/100
37/37 - 0s - loss: 81.7180 - val_loss: 209.7603 - 71ms/epoch - 2ms/step
Epoch 7/100
37/37 - 0s - loss: 74.8489 - val_loss: 97.2464 - 64ms/epoch - 2ms/step
Epoch 8/100
37/37 - 0s - loss: 70.2466 - val_loss: 102.9716 - 69ms/epoch - 2ms/step
Epoch 9/100
37/37 - 0s - loss: 84.4998 - val_loss: 120.7788 - 66ms/epoch - 2ms/step
Epoch 10/100
37/37 - 0s - loss: 84.2554 - val_loss: 51.5239 - 76ms/epoch - 2ms/step
Epoch 11/100
37/37 - 0s - loss: 82.7028 - val_loss: 63.9092 - 95ms/epoch - 3ms/step
Epoch 12/100
37/37 - 0s - loss: 81.1849 - val_loss: 157.6429 - 69ms/epoch - 2ms/step
Epoch 13/100
37/37 - 0s - loss: 67.5980 - val_loss: 93.7308 - 85ms/epoch - 2ms/step
Epoch 14/100
37/37 - 0s - loss: 95.7322 - val_loss: 47.3726 - 80ms/epoch - 2ms/step
Epoch 15/100
37/37 - 0s - loss: 130.0460 - val_loss: 147.8702 - 76ms/epoch - 2ms/step
Epoch 16/100
37/37 - 0s - loss: 62.5334 - val_loss: 64.7696 - 66ms/epoch - 2ms/step
Epoch 17/100
37/37 - 0s - loss: 46.6029 - val_loss: 25.6011 - 72ms/epoch - 2ms/step
Epoch 18/100
37/37 - 0s - loss: 117.4214 - val_loss: 36.4905 - 65ms/epoch - 2ms/step
Epoch 19/100
37/37 - 0s - loss: 45.7278 - val_loss: 222.9618 - 74ms/epoch - 2ms/step
Epoch 20/100
37/37 - 0s - loss: 86.3822 - val_loss: 153.3152 - 67ms/epoch - 2ms/step
Epoch 21/100
37/37 - 0s - loss: 49.1817 - val_loss: 32.7454 - 67ms/epoch - 2ms/step
Epoch 22/100
37/37 - 0s - loss: 88.3020 - val_loss: 49.0728 - 82ms/epoch - 2ms/step
Epoch 23/100
37/37 - 0s - loss: 123.6417 - val_loss: 16.1427 - 75ms/epoch - 2ms/step
Epoch 24/100
37/37 - 0s - loss: 140.2984 - val_loss: 125.4936 - 92ms/epoch - 2ms/step
Epoch 25/100
37/37 - 0s - loss: 81.8718 - val_loss: 28.7978 - 80ms/epoch - 2ms/step
Epoch 26/100
37/37 - 0s - loss: 97.1525 - val_loss: 84.2124 - 74ms/epoch - 2ms/step
Epoch 27/100
37/37 - 0s - loss: 81.8087 - val_loss: 59.0468 - 76ms/epoch - 2ms/step
Epoch 28/100
37/37 - 0s - loss: 85.1673 - val_loss: 25.2971 - 76ms/epoch - 2ms/step
Epoch 29/100
37/37 - 0s - loss: 71.8622 - val_loss: 138.9356 - 80ms/epoch - 2ms/step
Epoch 30/100
37/37 - 0s - loss: 71.2251 - val_loss: 49.1379 - 83ms/epoch - 2ms/step
Epoch 31/100
37/37 - 0s - loss: 71.5752 - val_loss: 55.2391 - 76ms/epoch - 2ms/step
Epoch 32/100
37/37 - 0s - loss: 45.8404 - val_loss: 49.0559 - 83ms/epoch - 2ms/step
Epoch 33/100
37/37 - 0s - loss: 46.0738 - val_loss: 49.4583 - 80ms/epoch - 2ms/step
Epoch 34/100
37/37 - 0s - loss: 45.7153 - val_loss: 37.0202 - 85ms/epoch - 2ms/step
Epoch 35/100
37/37 - 0s - loss: 44.0467 - val_loss: 30.9112 - 64ms/epoch - 2ms/step
Epoch 36/100
37/37 - 0s - loss: 68.8014 - val_loss: 146.4782 - 79ms/epoch - 2ms/step
Epoch 37/100
37/37 - 0s - loss: 84.9331 - val_loss: 101.8054 - 83ms/epoch - 2ms/step
Epoch 38/100
37/37 - 0s - loss: 81.8781 - val_loss: 98.1598 - 84ms/epoch - 2ms/step
Epoch 39/100
37/37 - 0s - loss: 83.1980 - val_loss: 126.6256 - 87ms/epoch - 2ms/step
Epoch 40/100
37/37 - 0s - loss: 83.5472 - val_loss: 80.5297 - 65ms/epoch - 2ms/step
Epoch 41/100
37/37 - 0s - loss: 82.2135 - val_loss: 65.5455 - 81ms/epoch - 2ms/step
Epoch 42/100
37/37 - 0s - loss: 81.8151 - val_loss: 64.8457 - 72ms/epoch - 2ms/step
Epoch 43/100
37/37 - 0s - loss: 60.8885 - val_loss: 163.7678 - 66ms/epoch - 2ms/step
Epoch 44/100
37/37 - 0s - loss: 43.7587 - val_loss: 7.2380 - 86ms/epoch - 2ms/step
Epoch 45/100
37/37 - 0s - loss: 91.3541 - val_loss: 19.1441 - 78ms/epoch - 2ms/step
Epoch 46/100
37/37 - 0s - loss: 66.6183 - val_loss: 64.2905 - 80ms/epoch - 2ms/step
Epoch 47/100
37/37 - 0s - loss: 45.4602 - val_loss: 116.9307 - 68ms/epoch - 2ms/step
Epoch 48/100
37/37 - 0s - loss: 52.6326 - val_loss: 39.7036 - 69ms/epoch - 2ms/step
Epoch 49/100
37/37 - 0s - loss: 46.0509 - val_loss: 37.1696 - 77ms/epoch - 2ms/step
Epoch 50/100
37/37 - 0s - loss: 46.1067 - val_loss: 53.3593 - 81ms/epoch - 2ms/step
Epoch 51/100
37/37 - 0s - loss: 45.5495 - val_loss: 61.4877 - 81ms/epoch - 2ms/step
Epoch 52/100
37/37 - 0s - loss: 44.9559 - val_loss: 34.3904 - 87ms/epoch - 2ms/step
Epoch 53/100
37/37 - 0s - loss: 45.2275 - val_loss: 53.7883 - 76ms/epoch - 2ms/step
Epoch 54/100
37/37 - 0s - loss: 45.6934 - val_loss: 63.1908 - 75ms/epoch - 2ms/step
Epoch 55/100
37/37 - 0s - loss: 46.1067 - val_loss: 10.2068 - 85ms/epoch - 2ms/step
Epoch 56/100
37/37 - 0s - loss: 82.5149 - val_loss: 61.9952 - 66ms/epoch - 2ms/step
Epoch 57/100
37/37 - 0s - loss: 45.8701 - val_loss: 36.5577 - 78ms/epoch - 2ms/step
Epoch 58/100
37/37 - 0s - loss: 45.7402 - val_loss: 85.4969 - 63ms/epoch - 2ms/step
Epoch 59/100
37/37 - 0s - loss: 63.6810 - val_loss: 65.9100 - 86ms/epoch - 2ms/step
Epoch 60/100
37/37 - 0s - loss: 44.1957 - val_loss: 51.6273 - 82ms/epoch - 2ms/step
Epoch 61/100
37/37 - 0s - loss: 46.6365 - val_loss: 31.7695 - 76ms/epoch - 2ms/step
Epoch 62/100
37/37 - 0s - loss: 45.4081 - val_loss: 44.0514 - 76ms/epoch - 2ms/step
Epoch 63/100
37/37 - 0s - loss: 46.8549 - val_loss: 127.2256 - 81ms/epoch - 2ms/step
Epoch 64/100
37/37 - 0s - loss: 69.1496 - val_loss: 51.3626 - 81ms/epoch - 2ms/step
Epoch 65/100
37/37 - 0s - loss: 45.1416 - val_loss: 48.3227 - 64ms/epoch - 2ms/step
Epoch 66/100
37/37 - 0s - loss: 45.0233 - val_loss: 34.2650 - 74ms/epoch - 2ms/step
Epoch 67/100
37/37 - 0s - loss: 72.7162 - val_loss: 76.3159 - 76ms/epoch - 2ms/step
Epoch 68/100
37/37 - 0s - loss: 28.7705 - val_loss: 29.2431 - 77ms/epoch - 2ms/step
Epoch 69/100
37/37 - 0s - loss: 149.0647 - val_loss: 46.3522 - 69ms/epoch - 2ms/step
Epoch 70/100
37/37 - 0s - loss: 98.0003 - val_loss: 258.0324 - 81ms/epoch - 2ms/step
Epoch 71/100
37/37 - 0s - loss: 56.0491 - val_loss: 58.0159 - 78ms/epoch - 2ms/step
Epoch 72/100
37/37 - 0s - loss: 45.0433 - val_loss: 28.3758 - 88ms/epoch - 2ms/step
Epoch 73/100
37/37 - 0s - loss: 45.4604 - val_loss: 20.7405 - 73ms/epoch - 2ms/step
Epoch 74/100
37/37 - 0s - loss: 44.7279 - val_loss: 50.9100 - 91ms/epoch - 2ms/step
Epoch 75/100
37/37 - 0s - loss: 45.1696 - val_loss: 35.7522 - 77ms/epoch - 2ms/step
Epoch 76/100
37/37 - 0s - loss: 43.3358 - val_loss: 68.7198 - 81ms/epoch - 2ms/step
Epoch 77/100
37/37 - 0s - loss: 46.5644 - val_loss: 32.3602 - 65ms/epoch - 2ms/step
Epoch 78/100
37/37 - 0s - loss: 46.1082 - val_loss: 6.9587 - 66ms/epoch - 2ms/step
Epoch 79/100
37/37 - 0s - loss: 67.9826 - val_loss: 14.9357 - 73ms/epoch - 2ms/step
Epoch 80/100
37/37 - 0s - loss: 101.1425 - val_loss: 7.1237 - 80ms/epoch - 2ms/step
Epoch 81/100
37/37 - 0s - loss: 52.3336 - val_loss: 39.1320 - 82ms/epoch - 2ms/step
Epoch 82/100
37/37 - 0s - loss: 45.6439 - val_loss: 37.2778 - 72ms/epoch - 2ms/step
Epoch 83/100
37/37 - 0s - loss: 42.2606 - val_loss: 64.6087 - 78ms/epoch - 2ms/step
Epoch 84/100
37/37 - 0s - loss: 45.4310 - val_loss: 51.2251 - 69ms/epoch - 2ms/step
Epoch 85/100
37/37 - 0s - loss: 45.9716 - val_loss: 33.5579 - 78ms/epoch - 2ms/step
Epoch 86/100
37/37 - 0s - loss: 45.8355 - val_loss: 35.1793 - 75ms/epoch - 2ms/step
Epoch 87/100
37/37 - 0s - loss: 45.2398 - val_loss: 21.3733 - 72ms/epoch - 2ms/step
Epoch 88/100
37/37 - 0s - loss: 64.9299 - val_loss: 251.5763 - 86ms/epoch - 2ms/step
Epoch 89/100
37/37 - 0s - loss: 58.6847 - val_loss: 34.3245 - 82ms/epoch - 2ms/step
Epoch 90/100
37/37 - 0s - loss: 61.2994 - val_loss: 108.2434 - 79ms/epoch - 2ms/step
Epoch 91/100
37/37 - 0s - loss: 84.6061 - val_loss: 107.5617 - 75ms/epoch - 2ms/step
Epoch 92/100
37/37 - 0s - loss: 83.8241 - val_loss: 44.2891 - 96ms/epoch - 3ms/step
Epoch 93/100
37/37 - 0s - loss: 83.3789 - val_loss: 84.6691 - 78ms/epoch - 2ms/step
Epoch 94/100
37/37 - 0s - loss: 84.0158 - val_loss: 104.5305 - 80ms/epoch - 2ms/step
Epoch 95/100
37/37 - 0s - loss: 83.3019 - val_loss: 111.9517 - 86ms/epoch - 2ms/step
Epoch 96/100
37/37 - 0s - loss: 69.3311 - val_loss: 42.9898 - 76ms/epoch - 2ms/step
Epoch 97/100
37/37 - 0s - loss: 79.7525 - val_loss: 118.2994 - 98ms/epoch - 3ms/step
Epoch 98/100
37/37 - 0s - loss: 150.7783 - val_loss: 41.6125 - 77ms/epoch - 2ms/step
Epoch 99/100
37/37 - 0s - loss: 135.5223 - val_loss: 113.9926 - 86ms/epoch - 2ms/step
Epoch 100/100
37/37 - 0s - loss: 133.6270 - val_loss: 207.9407 - 81ms/epoch - 2ms/step
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 normalization (Normalizatio  (None, 288)              577       
 n)                                                              
                                                                 
 dense (Dense)               (None, 1)                 289       
                                                                 
=================================================================
Total params: 866
Trainable params: 289
Non-trainable params: 577
_________________________________________________________________

from keras.models import Sequential
from keras.layers import Dense
from keras import metrics
import tensorflow as tf

def r2(y_true, y_pred):
    from keras import backend as K
    SS_res =  K.sum(K.square( y_true-y_pred ))
    SS_tot = K.sum(K.square( y_true - K.mean(y_true) ) )
    return ( 1 - SS_res/(SS_tot + K.epsilon()) )

#Create our model using sequential mode
model = Sequential()
model.add(tf.keras.layers.Normalization(axis=-1))
model.add(Dense(units=1))
model.compile(optimizer='adam', loss='mean_absolute_error', metrics=[r2])

model.fit( X_train, y_train, epochs=100, verbose=2, validation_split = 0.2)
model.summary()

Epoch 1/100
37/37 - 1s - loss: 355.1505 - r2: -9.4646e+05 - val_loss: 190.2667 - val_r2: -2.9509e+05 - 826ms/epoch - 22ms/step
Epoch 2/100
37/37 - 0s - loss: 72.4606 - r2: -5.6748e+04 - val_loss: 25.4438 - val_r2: -6.8721e+03 - 65ms/epoch - 2ms/step
Epoch 3/100
37/37 - 0s - loss: 20.0344 - r2: -4.6832e+03 - val_loss: 18.9579 - val_r2: -4.5034e+03 - 77ms/epoch - 2ms/step
Epoch 4/100
37/37 - 0s - loss: 16.9299 - r2: -3.3164e+03 - val_loss: 16.6163 - val_r2: -3.3528e+03 - 80ms/epoch - 2ms/step
Epoch 5/100
37/37 - 0s - loss: 14.7259 - r2: -2.5158e+03 - val_loss: 14.1100 - val_r2: -2.5527e+03 - 82ms/epoch - 2ms/step
Epoch 6/100
37/37 - 0s - loss: 11.6185 - r2: -1.5714e+03 - val_loss: 10.7319 - val_r2: -1.3975e+03 - 71ms/epoch - 2ms/step
Epoch 7/100
37/37 - 0s - loss: 8.6401 - r2: -8.8282e+02 - val_loss: 7.6083 - val_r2: -7.0088e+02 - 94ms/epoch - 3ms/step
Epoch 8/100
37/37 - 0s - loss: 5.7721 - r2: -4.1462e+02 - val_loss: 4.5022 - val_r2: -2.4888e+02 - 74ms/epoch - 2ms/step
Epoch 9/100
37/37 - 0s - loss: 3.3505 - r2: -1.4108e+02 - val_loss: 3.0097 - val_r2: -1.3140e+02 - 71ms/epoch - 2ms/step
Epoch 10/100
37/37 - 0s - loss: 2.1553 - r2: -6.5851e+01 - val_loss: 1.9778 - val_r2: -6.9413e+01 - 80ms/epoch - 2ms/step
Epoch 11/100
37/37 - 0s - loss: 1.9882 - r2: -5.7675e+01 - val_loss: 2.2088 - val_r2: -1.0363e+02 - 70ms/epoch - 2ms/step
Epoch 12/100
37/37 - 0s - loss: 2.0190 - r2: -5.4628e+01 - val_loss: 1.7860 - val_r2: -7.4969e+01 - 77ms/epoch - 2ms/step
Epoch 13/100
37/37 - 0s - loss: 1.8813 - r2: -5.0003e+01 - val_loss: 2.1725 - val_r2: -9.6949e+01 - 87ms/epoch - 2ms/step
Epoch 14/100
37/37 - 0s - loss: 1.6572 - r2: -4.7300e+01 - val_loss: 1.7413 - val_r2: -7.6229e+01 - 68ms/epoch - 2ms/step
Epoch 15/100
37/37 - 0s - loss: 1.6704 - r2: -4.4853e+01 - val_loss: 1.8515 - val_r2: -4.7344e+01 - 84ms/epoch - 2ms/step
Epoch 16/100
37/37 - 0s - loss: 1.9507 - r2: -4.7104e+01 - val_loss: 1.5440 - val_r2: -4.6267e+01 - 78ms/epoch - 2ms/step
Epoch 17/100
37/37 - 0s - loss: 1.7918 - r2: -4.2032e+01 - val_loss: 2.0625 - val_r2: -4.5285e+01 - 83ms/epoch - 2ms/step
Epoch 18/100
37/37 - 0s - loss: 2.1079 - r2: -4.9106e+01 - val_loss: 1.3987 - val_r2: -4.9343e+01 - 75ms/epoch - 2ms/step
Epoch 19/100
37/37 - 0s - loss: 1.6797 - r2: -3.8484e+01 - val_loss: 1.6010 - val_r2: -6.1286e+01 - 90ms/epoch - 2ms/step
Epoch 20/100
37/37 - 0s - loss: 1.4548 - r2: -3.5214e+01 - val_loss: 1.3611 - val_r2: -4.2450e+01 - 80ms/epoch - 2ms/step
Epoch 21/100
37/37 - 0s - loss: 1.4217 - r2: -3.2836e+01 - val_loss: 1.7635 - val_r2: -6.5155e+01 - 85ms/epoch - 2ms/step
Epoch 22/100
37/37 - 0s - loss: 1.4356 - r2: -3.5358e+01 - val_loss: 1.3794 - val_r2: -3.8754e+01 - 76ms/epoch - 2ms/step
Epoch 23/100
37/37 - 0s - loss: 1.6295 - r2: -3.4610e+01 - val_loss: 1.8503 - val_r2: -6.4173e+01 - 73ms/epoch - 2ms/step
Epoch 24/100
37/37 - 0s - loss: 1.4739 - r2: -3.4697e+01 - val_loss: 1.4014 - val_r2: -4.8938e+01 - 83ms/epoch - 2ms/step
Epoch 25/100
37/37 - 0s - loss: 1.4994 - r2: -3.3625e+01 - val_loss: 1.7837 - val_r2: -6.1207e+01 - 78ms/epoch - 2ms/step
Epoch 26/100
37/37 - 0s - loss: 1.3629 - r2: -3.2870e+01 - val_loss: 1.2624 - val_r2: -3.9014e+01 - 91ms/epoch - 2ms/step
Epoch 27/100
37/37 - 0s - loss: 1.3159 - r2: -2.8338e+01 - val_loss: 1.3699 - val_r2: -4.5740e+01 - 71ms/epoch - 2ms/step
Epoch 28/100
37/37 - 0s - loss: 1.4017 - r2: -2.9479e+01 - val_loss: 2.0512 - val_r2: -3.7733e+01 - 88ms/epoch - 2ms/step
Epoch 29/100
37/37 - 0s - loss: 1.4739 - r2: -3.3017e+01 - val_loss: 1.8081 - val_r2: -3.3231e+01 - 70ms/epoch - 2ms/step
Epoch 30/100
37/37 - 0s - loss: 1.3530 - r2: -2.8794e+01 - val_loss: 1.2498 - val_r2: -3.4292e+01 - 71ms/epoch - 2ms/step
Epoch 31/100
37/37 - 0s - loss: 1.3052 - r2: -2.9230e+01 - val_loss: 1.4935 - val_r2: -4.7340e+01 - 81ms/epoch - 2ms/step
Epoch 32/100
37/37 - 0s - loss: 1.4997 - r2: -3.1964e+01 - val_loss: 1.6307 - val_r2: -5.0497e+01 - 82ms/epoch - 2ms/step
Epoch 33/100
37/37 - 0s - loss: 1.3356 - r2: -2.7551e+01 - val_loss: 1.7173 - val_r2: -3.0840e+01 - 85ms/epoch - 2ms/step
Epoch 34/100
37/37 - 0s - loss: 1.6412 - r2: -3.2541e+01 - val_loss: 1.4812 - val_r2: -2.8111e+01 - 71ms/epoch - 2ms/step
Epoch 35/100
37/37 - 0s - loss: 1.5440 - r2: -3.2052e+01 - val_loss: 1.2114 - val_r2: -3.0751e+01 - 80ms/epoch - 2ms/step
Epoch 36/100
37/37 - 0s - loss: 1.3084 - r2: -2.7053e+01 - val_loss: 1.1988 - val_r2: -3.0865e+01 - 81ms/epoch - 2ms/step
Epoch 37/100
37/37 - 0s - loss: 1.3044 - r2: -2.5962e+01 - val_loss: 1.3619 - val_r2: -2.7614e+01 - 74ms/epoch - 2ms/step
Epoch 38/100
37/37 - 0s - loss: 1.2547 - r2: -2.5255e+01 - val_loss: 1.1836 - val_r2: -3.1146e+01 - 73ms/epoch - 2ms/step
Epoch 39/100
37/37 - 0s - loss: 1.2947 - r2: -2.5581e+01 - val_loss: 1.4510 - val_r2: -2.7187e+01 - 76ms/epoch - 2ms/step
Epoch 40/100
37/37 - 0s - loss: 1.2923 - r2: -2.3912e+01 - val_loss: 1.5723 - val_r2: -2.7390e+01 - 69ms/epoch - 2ms/step
Epoch 41/100
37/37 - 0s - loss: 1.2649 - r2: -2.4538e+01 - val_loss: 1.2192 - val_r2: -3.2797e+01 - 80ms/epoch - 2ms/step
Epoch 42/100
37/37 - 0s - loss: 1.3609 - r2: -2.5760e+01 - val_loss: 1.9855 - val_r2: -3.3683e+01 - 89ms/epoch - 2ms/step
Epoch 43/100
37/37 - 0s - loss: 1.4007 - r2: -2.5319e+01 - val_loss: 1.2609 - val_r2: -3.2965e+01 - 76ms/epoch - 2ms/step
Epoch 44/100
37/37 - 0s - loss: 1.2599 - r2: -2.2131e+01 - val_loss: 1.3658 - val_r2: -2.5270e+01 - 78ms/epoch - 2ms/step
Epoch 45/100
37/37 - 0s - loss: 1.2158 - r2: -2.2139e+01 - val_loss: 1.2596 - val_r2: -2.5546e+01 - 71ms/epoch - 2ms/step
Epoch 46/100
37/37 - 0s - loss: 1.3602 - r2: -2.4587e+01 - val_loss: 1.2226 - val_r2: -2.5057e+01 - 91ms/epoch - 2ms/step
Epoch 47/100
37/37 - 0s - loss: 1.1958 - r2: -2.0915e+01 - val_loss: 1.3164 - val_r2: -2.4304e+01 - 73ms/epoch - 2ms/step
Epoch 48/100
37/37 - 0s - loss: 1.1744 - r2: -2.1883e+01 - val_loss: 1.1709 - val_r2: -2.6255e+01 - 73ms/epoch - 2ms/step
Epoch 49/100
37/37 - 0s - loss: 1.2126 - r2: -2.2147e+01 - val_loss: 1.2077 - val_r2: -2.4420e+01 - 80ms/epoch - 2ms/step
Epoch 50/100
37/37 - 0s - loss: 1.1510 - r2: -2.1154e+01 - val_loss: 1.1561 - val_r2: -2.7689e+01 - 86ms/epoch - 2ms/step
Epoch 51/100
37/37 - 0s - loss: 1.1131 - r2: -1.9751e+01 - val_loss: 1.4260 - val_r2: -3.6163e+01 - 82ms/epoch - 2ms/step
Epoch 52/100
37/37 - 0s - loss: 1.4734 - r2: -2.7226e+01 - val_loss: 1.2395 - val_r2: -2.3802e+01 - 84ms/epoch - 2ms/step
Epoch 53/100
37/37 - 0s - loss: 1.2630 - r2: -2.2467e+01 - val_loss: 1.5405 - val_r2: -2.4448e+01 - 96ms/epoch - 3ms/step
Epoch 54/100
37/37 - 0s - loss: 1.2786 - r2: -2.0858e+01 - val_loss: 1.1949 - val_r2: -2.7795e+01 - 70ms/epoch - 2ms/step
Epoch 55/100
37/37 - 0s - loss: 1.4157 - r2: -2.3954e+01 - val_loss: 1.2763 - val_r2: -2.2481e+01 - 70ms/epoch - 2ms/step
Epoch 56/100
37/37 - 0s - loss: 1.1565 - r2: -1.9474e+01 - val_loss: 1.2357 - val_r2: -2.8131e+01 - 78ms/epoch - 2ms/step
Epoch 57/100
37/37 - 0s - loss: 1.3165 - r2: -2.3790e+01 - val_loss: 1.1938 - val_r2: -2.7622e+01 - 79ms/epoch - 2ms/step
Epoch 58/100
37/37 - 0s - loss: 1.2390 - r2: -2.0249e+01 - val_loss: 1.1562 - val_r2: -2.3982e+01 - 89ms/epoch - 2ms/step
Epoch 59/100
37/37 - 0s - loss: 1.2480 - r2: -2.0389e+01 - val_loss: 1.1937 - val_r2: -2.6507e+01 - 74ms/epoch - 2ms/step
Epoch 60/100
37/37 - 0s - loss: 1.3407 - r2: -2.1839e+01 - val_loss: 1.2384 - val_r2: -2.7895e+01 - 95ms/epoch - 3ms/step
Epoch 61/100
37/37 - 0s - loss: 1.1823 - r2: -1.9913e+01 - val_loss: 1.4024 - val_r2: -2.2328e+01 - 84ms/epoch - 2ms/step
Epoch 62/100
37/37 - 0s - loss: 1.1116 - r2: -1.8633e+01 - val_loss: 1.3786 - val_r2: -2.2028e+01 - 78ms/epoch - 2ms/step
Epoch 63/100
37/37 - 0s - loss: 1.6215 - r2: -2.9055e+01 - val_loss: 1.8527 - val_r2: -3.0105e+01 - 71ms/epoch - 2ms/step
Epoch 64/100
37/37 - 0s - loss: 1.2890 - r2: -2.2914e+01 - val_loss: 2.2517 - val_r2: -4.1651e+01 - 81ms/epoch - 2ms/step
Epoch 65/100
37/37 - 0s - loss: 1.4926 - r2: -2.3735e+01 - val_loss: 1.3060 - val_r2: -2.7523e+01 - 75ms/epoch - 2ms/step
Epoch 66/100
37/37 - 0s - loss: 1.0768 - r2: -1.6794e+01 - val_loss: 2.0318 - val_r2: -3.4483e+01 - 67ms/epoch - 2ms/step
Epoch 67/100
37/37 - 0s - loss: 1.1267 - r2: -1.7434e+01 - val_loss: 1.1696 - val_r2: -2.3706e+01 - 80ms/epoch - 2ms/step
Epoch 68/100
37/37 - 0s - loss: 1.0895 - r2: -1.8077e+01 - val_loss: 1.2544 - val_r2: -2.6386e+01 - 68ms/epoch - 2ms/step
Epoch 69/100
37/37 - 0s - loss: 1.1382 - r2: -1.7417e+01 - val_loss: 1.4818 - val_r2: -3.3265e+01 - 76ms/epoch - 2ms/step
Epoch 70/100
37/37 - 0s - loss: 1.1501 - r2: -1.7860e+01 - val_loss: 1.3900 - val_r2: -2.9791e+01 - 81ms/epoch - 2ms/step
Epoch 71/100
37/37 - 0s - loss: 1.0977 - r2: -1.6928e+01 - val_loss: 1.1348 - val_r2: -2.0971e+01 - 69ms/epoch - 2ms/step
Epoch 72/100
37/37 - 0s - loss: 1.0731 - r2: -1.6784e+01 - val_loss: 1.3158 - val_r2: -2.8019e+01 - 78ms/epoch - 2ms/step
Epoch 73/100
37/37 - 0s - loss: 1.1518 - r2: -1.7669e+01 - val_loss: 1.1415 - val_r2: -2.0724e+01 - 69ms/epoch - 2ms/step
Epoch 74/100
37/37 - 0s - loss: 1.0428 - r2: -1.6114e+01 - val_loss: 1.1470 - val_r2: -2.2800e+01 - 82ms/epoch - 2ms/step
Epoch 75/100
37/37 - 0s - loss: 1.1218 - r2: -1.6293e+01 - val_loss: 1.1105 - val_r2: -2.1247e+01 - 72ms/epoch - 2ms/step
Epoch 76/100
37/37 - 0s - loss: 1.0988 - r2: -1.5958e+01 - val_loss: 1.1656 - val_r2: -2.2803e+01 - 77ms/epoch - 2ms/step
Epoch 77/100
37/37 - 0s - loss: 1.1779 - r2: -1.7411e+01 - val_loss: 2.4004 - val_r2: -4.9047e+01 - 78ms/epoch - 2ms/step
Epoch 78/100
37/37 - 0s - loss: 1.4811 - r2: -2.3133e+01 - val_loss: 1.1567 - val_r2: -2.1918e+01 - 69ms/epoch - 2ms/step
Epoch 79/100
37/37 - 0s - loss: 1.3526 - r2: -2.0490e+01 - val_loss: 1.9884 - val_r2: -4.7201e+01 - 74ms/epoch - 2ms/step
Epoch 80/100
37/37 - 0s - loss: 1.4266 - r2: -2.2374e+01 - val_loss: 2.3830 - val_r2: -4.8639e+01 - 84ms/epoch - 2ms/step
Epoch 81/100
37/37 - 0s - loss: 1.3391 - r2: -2.0407e+01 - val_loss: 2.0779 - val_r2: -5.0130e+01 - 85ms/epoch - 2ms/step
Epoch 82/100
37/37 - 0s - loss: 1.2354 - r2: -2.0801e+01 - val_loss: 1.6245 - val_r2: -2.5247e+01 - 72ms/epoch - 2ms/step
Epoch 83/100
37/37 - 0s - loss: 1.1462 - r2: -1.6617e+01 - val_loss: 1.1847 - val_r2: -1.9231e+01 - 85ms/epoch - 2ms/step
Epoch 84/100
37/37 - 0s - loss: 1.1585 - r2: -1.6167e+01 - val_loss: 1.2066 - val_r2: -2.2864e+01 - 73ms/epoch - 2ms/step
Epoch 85/100
37/37 - 0s - loss: 1.0043 - r2: -1.3775e+01 - val_loss: 1.1308 - val_r2: -2.1076e+01 - 72ms/epoch - 2ms/step
Epoch 86/100
37/37 - 0s - loss: 1.0747 - r2: -1.5015e+01 - val_loss: 1.1764 - val_r2: -1.9037e+01 - 80ms/epoch - 2ms/step
Epoch 87/100
37/37 - 0s - loss: 1.0467 - r2: -1.4848e+01 - val_loss: 1.6271 - val_r2: -3.4642e+01 - 73ms/epoch - 2ms/step
Epoch 88/100
37/37 - 0s - loss: 1.6162 - r2: -2.8362e+01 - val_loss: 1.5067 - val_r2: -2.3191e+01 - 72ms/epoch - 2ms/step
Epoch 89/100
37/37 - 0s - loss: 1.4198 - r2: -2.1559e+01 - val_loss: 1.4599 - val_r2: -2.2404e+01 - 65ms/epoch - 2ms/step
Epoch 90/100
37/37 - 0s - loss: 1.0455 - r2: -1.4796e+01 - val_loss: 1.5309 - val_r2: -2.3689e+01 - 75ms/epoch - 2ms/step
Epoch 91/100
37/37 - 0s - loss: 1.0276 - r2: -1.3598e+01 - val_loss: 1.3207 - val_r2: -2.5536e+01 - 75ms/epoch - 2ms/step
Epoch 92/100
37/37 - 0s - loss: 0.9909 - r2: -1.4048e+01 - val_loss: 1.0958 - val_r2: -1.9116e+01 - 81ms/epoch - 2ms/step
Epoch 93/100
37/37 - 0s - loss: 1.0332 - r2: -1.4157e+01 - val_loss: 1.1048 - val_r2: -1.9316e+01 - 70ms/epoch - 2ms/step
Epoch 94/100
37/37 - 0s - loss: 1.0126 - r2: -1.3294e+01 - val_loss: 1.0880 - val_r2: -1.8810e+01 - 71ms/epoch - 2ms/step
Epoch 95/100
37/37 - 0s - loss: 1.0271 - r2: -1.3112e+01 - val_loss: 1.3453 - val_r2: -2.0197e+01 - 65ms/epoch - 2ms/step
Epoch 96/100
37/37 - 0s - loss: 1.1322 - r2: -1.5226e+01 - val_loss: 1.1092 - val_r2: -1.9649e+01 - 80ms/epoch - 2ms/step
Epoch 97/100
37/37 - 0s - loss: 1.0259 - r2: -1.4178e+01 - val_loss: 1.2392 - val_r2: -2.2552e+01 - 74ms/epoch - 2ms/step
Epoch 98/100
37/37 - 0s - loss: 1.0047 - r2: -1.3929e+01 - val_loss: 1.1725 - val_r2: -1.8385e+01 - 84ms/epoch - 2ms/step
Epoch 99/100
37/37 - 0s - loss: 0.9695 - r2: -1.3726e+01 - val_loss: 1.0929 - val_r2: -1.8385e+01 - 98ms/epoch - 3ms/step
Epoch 100/100
37/37 - 0s - loss: 1.2929 - r2: -1.9990e+01 - val_loss: 1.6890 - val_r2: -2.7182e+01 - 77ms/epoch - 2ms/step
Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 normalization_1 (Normalizat  (None, 288)              577       
 ion)                                                            
                                                                 
 dense_1 (Dense)             (None, 1)                 289       
                                                                 
=================================================================
Total params: 866
Trainable params: 289
Non-trainable params: 577
_________________________________________________________________

# Alternate Sequential syntax, with some additional data
import tensorflow as tf
altmodel = tf.keras.Sequential([
    tf.keras.layers.Normalization(axis=-1),
    tf.keras.layers.Dense(100, activation='relu'),
    tf.keras.layers.Dense(100, activation='relu'),
    tf.keras.layers.Dense(units=1),
])
altmodel.compile(loss='mean_absolute_error', optimizer='adam', metrics=[r2])
altmodel.fit( X_train, y_train, epochs=100, verbose=2, validation_split = 0.2)
altmodel.summary()
#Can predict and then evaluate. 
y_pred_train_alt = altmodel.predict(X_train)
y_pred_test_alt = altmodel.predict(X_test)

Epoch 1/100
37/37 - 1s - loss: 14.7804 - r2: -4.1397e+03 - val_loss: 7.2279 - val_r2: -4.4522e+02 - 784ms/epoch - 21ms/step
Epoch 2/100
37/37 - 0s - loss: 6.4071 - r2: -4.0960e+02 - val_loss: 6.2704 - val_r2: -3.2853e+02 - 99ms/epoch - 3ms/step
Epoch 3/100
37/37 - 0s - loss: 6.9593 - r2: -4.3096e+02 - val_loss: 3.6507 - val_r2: -1.1908e+02 - 100ms/epoch - 3ms/step
Epoch 4/100
37/37 - 0s - loss: 4.0448 - r2: -1.7119e+02 - val_loss: 4.8484 - val_r2: -1.9517e+02 - 92ms/epoch - 2ms/step
Epoch 5/100
37/37 - 0s - loss: 5.6182 - r2: -2.7335e+02 - val_loss: 1.4258 - val_r2: -2.3183e+01 - 104ms/epoch - 3ms/step
Epoch 6/100
37/37 - 0s - loss: 4.3751 - r2: -1.6391e+02 - val_loss: 1.8319 - val_r2: -3.9956e+01 - 96ms/epoch - 3ms/step
Epoch 7/100
37/37 - 0s - loss: 6.3957 - r2: -5.4834e+02 - val_loss: 9.8020 - val_r2: -7.9400e+02 - 90ms/epoch - 2ms/step
Epoch 8/100
37/37 - 0s - loss: 8.1412 - r2: -5.8854e+02 - val_loss: 8.9223 - val_r2: -6.3433e+02 - 118ms/epoch - 3ms/step
Epoch 9/100
37/37 - 0s - loss: 4.5717 - r2: -3.3393e+02 - val_loss: 1.0295 - val_r2: -1.3045e+01 - 101ms/epoch - 3ms/step
Epoch 10/100
37/37 - 0s - loss: 4.1206 - r2: -2.0298e+02 - val_loss: 14.0824 - val_r2: -1.5621e+03 - 91ms/epoch - 2ms/step
Epoch 11/100
37/37 - 0s - loss: 5.9491 - r2: -3.3559e+02 - val_loss: 1.0511 - val_r2: -1.5103e+01 - 97ms/epoch - 3ms/step
Epoch 12/100
37/37 - 0s - loss: 8.3444 - r2: -6.9866e+02 - val_loss: 12.3003 - val_r2: -1.1805e+03 - 100ms/epoch - 3ms/step
Epoch 13/100
37/37 - 0s - loss: 10.8001 - r2: -9.7253e+02 - val_loss: 13.6985 - val_r2: -1.4451e+03 - 91ms/epoch - 2ms/step
Epoch 14/100
37/37 - 0s - loss: 9.9140 - r2: -8.1723e+02 - val_loss: 2.0036 - val_r2: -4.4759e+01 - 110ms/epoch - 3ms/step
Epoch 15/100
37/37 - 0s - loss: 9.5234 - r2: -7.4071e+02 - val_loss: 6.6051 - val_r2: -3.5045e+02 - 91ms/epoch - 2ms/step
Epoch 16/100
37/37 - 0s - loss: 8.7733 - r2: -6.0001e+02 - val_loss: 12.2833 - val_r2: -1.1762e+03 - 109ms/epoch - 3ms/step
Epoch 17/100
37/37 - 0s - loss: 8.4753 - r2: -5.8430e+02 - val_loss: 10.1909 - val_r2: -8.3424e+02 - 94ms/epoch - 3ms/step
Epoch 18/100
37/37 - 0s - loss: 7.9609 - r2: -5.5093e+02 - val_loss: 3.8174 - val_r2: -1.2977e+02 - 98ms/epoch - 3ms/step
Epoch 19/100
37/37 - 0s - loss: 5.3270 - r2: -2.6629e+02 - val_loss: 3.1693 - val_r2: -9.1347e+01 - 98ms/epoch - 3ms/step
Epoch 20/100
37/37 - 0s - loss: 3.6391 - r2: -1.1971e+02 - val_loss: 1.9633 - val_r2: -3.0561e+01 - 101ms/epoch - 3ms/step
Epoch 21/100
37/37 - 0s - loss: 4.5496 - r2: -2.3961e+02 - val_loss: 10.8011 - val_r2: -9.0074e+02 - 104ms/epoch - 3ms/step
Epoch 22/100
37/37 - 0s - loss: 4.7209 - r2: -1.8531e+02 - val_loss: 3.2146 - val_r2: -7.9610e+01 - 100ms/epoch - 3ms/step
Epoch 23/100
37/37 - 0s - loss: 4.3990 - r2: -1.5262e+02 - val_loss: 3.5896 - val_r2: -1.0679e+02 - 105ms/epoch - 3ms/step
Epoch 24/100
37/37 - 0s - loss: 3.9595 - r2: -1.2561e+02 - val_loss: 1.0165 - val_r2: -1.0062e+01 - 113ms/epoch - 3ms/step
Epoch 25/100
37/37 - 0s - loss: 1.2295 - r2: -1.6816e+01 - val_loss: 2.5838 - val_r2: -5.6809e+01 - 105ms/epoch - 3ms/step
Epoch 26/100
37/37 - 0s - loss: 2.3656 - r2: -5.1829e+01 - val_loss: 0.5281 - val_r2: -2.3242e+00 - 93ms/epoch - 3ms/step
Epoch 27/100
37/37 - 0s - loss: 3.9184 - r2: -1.6453e+02 - val_loss: 1.4938 - val_r2: -2.2279e+01 - 93ms/epoch - 3ms/step
Epoch 28/100
37/37 - 0s - loss: 3.0941 - r2: -8.9662e+01 - val_loss: 1.8549 - val_r2: -2.7524e+01 - 96ms/epoch - 3ms/step
Epoch 29/100
37/37 - 0s - loss: 4.0704 - r2: -1.8723e+02 - val_loss: 11.0759 - val_r2: -9.4438e+02 - 96ms/epoch - 3ms/step
Epoch 30/100
37/37 - 0s - loss: 4.3475 - r2: -1.6315e+02 - val_loss: 4.1581 - val_r2: -1.3059e+02 - 90ms/epoch - 2ms/step
Epoch 31/100
37/37 - 0s - loss: 3.8052 - r2: -1.2190e+02 - val_loss: 4.9504 - val_r2: -1.8484e+02 - 92ms/epoch - 2ms/step
Epoch 32/100
37/37 - 0s - loss: 3.6763 - r2: -1.0713e+02 - val_loss: 1.6915 - val_r2: -2.3214e+01 - 114ms/epoch - 3ms/step
Epoch 33/100
37/37 - 0s - loss: 3.0238 - r2: -9.2015e+01 - val_loss: 0.9948 - val_r2: -9.4615e+00 - 95ms/epoch - 3ms/step
Epoch 34/100
37/37 - 0s - loss: 4.1872 - r2: -1.5606e+02 - val_loss: 5.7390 - val_r2: -2.5528e+02 - 108ms/epoch - 3ms/step
Epoch 35/100
37/37 - 0s - loss: 5.4563 - r2: -2.3696e+02 - val_loss: 1.8160 - val_r2: -2.6878e+01 - 99ms/epoch - 3ms/step
Epoch 36/100
37/37 - 0s - loss: 5.0562 - r2: -2.3707e+02 - val_loss: 5.4249 - val_r2: -2.3117e+02 - 87ms/epoch - 2ms/step
Epoch 37/100
37/37 - 0s - loss: 4.0670 - r2: -1.4545e+02 - val_loss: 0.7556 - val_r2: -5.1643e+00 - 102ms/epoch - 3ms/step
Epoch 38/100
37/37 - 0s - loss: 2.1800 - r2: -6.6878e+01 - val_loss: 2.4198 - val_r2: -4.9567e+01 - 96ms/epoch - 3ms/step
Epoch 39/100
37/37 - 0s - loss: 1.6227 - r2: -2.0769e+01 - val_loss: 1.8895 - val_r2: -2.9481e+01 - 102ms/epoch - 3ms/step
Epoch 40/100
37/37 - 0s - loss: 1.4320 - r2: -1.8623e+01 - val_loss: 0.3714 - val_r2: -1.1311e+00 - 107ms/epoch - 3ms/step
Epoch 41/100
37/37 - 0s - loss: 1.1947 - r2: -1.5619e+01 - val_loss: 2.4090 - val_r2: -4.7308e+01 - 99ms/epoch - 3ms/step
Epoch 42/100
37/37 - 0s - loss: 1.8249 - r2: -3.5785e+01 - val_loss: 0.8397 - val_r2: -6.1637e+00 - 87ms/epoch - 2ms/step
Epoch 43/100
37/37 - 0s - loss: 1.0834 - r2: -1.0672e+01 - val_loss: 0.4278 - val_r2: -1.5788e+00 - 103ms/epoch - 3ms/step
Epoch 44/100
37/37 - 0s - loss: 1.4248 - r2: -3.3604e+01 - val_loss: 2.1557 - val_r2: -3.6034e+01 - 97ms/epoch - 3ms/step
Epoch 45/100
37/37 - 0s - loss: 1.5884 - r2: -2.0027e+01 - val_loss: 1.3180 - val_r2: -1.5065e+01 - 94ms/epoch - 3ms/step
Epoch 46/100
37/37 - 0s - loss: 1.8736 - r2: -3.7267e+01 - val_loss: 1.0554 - val_r2: -9.7051e+00 - 100ms/epoch - 3ms/step
Epoch 47/100
37/37 - 0s - loss: 3.7636 - r2: -1.3601e+02 - val_loss: 1.6264 - val_r2: -2.8172e+01 - 94ms/epoch - 3ms/step
Epoch 48/100
37/37 - 0s - loss: 3.5765 - r2: -1.1773e+02 - val_loss: 4.0436 - val_r2: -1.3326e+02 - 101ms/epoch - 3ms/step
Epoch 49/100
37/37 - 0s - loss: 1.9240 - r2: -3.4255e+01 - val_loss: 1.3053 - val_r2: -1.3135e+01 - 99ms/epoch - 3ms/step
Epoch 50/100
37/37 - 0s - loss: 1.5022 - r2: -1.6608e+01 - val_loss: 1.4238 - val_r2: -2.1942e+01 - 105ms/epoch - 3ms/step
Epoch 51/100
37/37 - 0s - loss: 1.9456 - r2: -6.3002e+01 - val_loss: 6.3944 - val_r2: -3.1072e+02 - 103ms/epoch - 3ms/step
Epoch 52/100
37/37 - 0s - loss: 2.8933 - r2: -8.4600e+01 - val_loss: 1.1214 - val_r2: -1.0220e+01 - 101ms/epoch - 3ms/step
Epoch 53/100
37/37 - 0s - loss: 2.3811 - r2: -5.7199e+01 - val_loss: 4.2020 - val_r2: -1.4038e+02 - 102ms/epoch - 3ms/step
Epoch 54/100
37/37 - 0s - loss: 1.7411 - r2: -2.7367e+01 - val_loss: 0.3733 - val_r2: -1.0603e+00 - 103ms/epoch - 3ms/step
Epoch 55/100
37/37 - 0s - loss: 1.3033 - r2: -1.5993e+01 - val_loss: 0.5918 - val_r2: -2.6233e+00 - 95ms/epoch - 3ms/step
Epoch 56/100
37/37 - 0s - loss: 2.0235 - r2: -4.5214e+01 - val_loss: 1.7575 - val_r2: -2.4859e+01 - 88ms/epoch - 2ms/step
Epoch 57/100
37/37 - 0s - loss: 2.9578 - r2: -8.0559e+01 - val_loss: 6.0201 - val_r2: -2.7488e+02 - 99ms/epoch - 3ms/step
Epoch 58/100
37/37 - 0s - loss: 1.5886 - r2: -2.8365e+01 - val_loss: 0.5092 - val_r2: -2.9337e+00 - 107ms/epoch - 3ms/step
Epoch 59/100
37/37 - 0s - loss: 0.9539 - r2: -1.1872e+01 - val_loss: 1.4655 - val_r2: -1.7221e+01 - 102ms/epoch - 3ms/step
Epoch 60/100
37/37 - 0s - loss: 1.2577 - r2: -1.3825e+01 - val_loss: 1.1363 - val_r2: -1.0055e+01 - 92ms/epoch - 2ms/step
Epoch 61/100
37/37 - 0s - loss: 1.2530 - r2: -1.2735e+01 - val_loss: 2.8243 - val_r2: -6.4006e+01 - 91ms/epoch - 2ms/step
Epoch 62/100
37/37 - 0s - loss: 2.6584 - r2: -7.3657e+01 - val_loss: 0.4199 - val_r2: -1.4324e+00 - 105ms/epoch - 3ms/step
Epoch 63/100
37/37 - 0s - loss: 1.1309 - r2: -1.0787e+01 - val_loss: 1.1720 - val_r2: -1.0414e+01 - 105ms/epoch - 3ms/step
Epoch 64/100
37/37 - 0s - loss: 1.5949 - r2: -2.5473e+01 - val_loss: 2.2937 - val_r2: -4.0207e+01 - 98ms/epoch - 3ms/step
Epoch 65/100
37/37 - 0s - loss: 1.3945 - r2: -1.8471e+01 - val_loss: 0.9140 - val_r2: -7.4867e+00 - 102ms/epoch - 3ms/step
Epoch 66/100
37/37 - 0s - loss: 1.2005 - r2: -1.1890e+01 - val_loss: 1.1984 - val_r2: -1.1772e+01 - 111ms/epoch - 3ms/step
Epoch 67/100
37/37 - 0s - loss: 1.1850 - r2: -1.1528e+01 - val_loss: 1.8111 - val_r2: -2.5158e+01 - 100ms/epoch - 3ms/step
Epoch 68/100
37/37 - 0s - loss: 1.5586 - r2: -3.2197e+01 - val_loss: 2.5344 - val_r2: -5.1185e+01 - 102ms/epoch - 3ms/step
Epoch 69/100
37/37 - 0s - loss: 2.1070 - r2: -3.5129e+01 - val_loss: 2.0777 - val_r2: -3.7266e+01 - 101ms/epoch - 3ms/step
Epoch 70/100
37/37 - 0s - loss: 2.0116 - r2: -3.6602e+01 - val_loss: 3.6790 - val_r2: -1.0855e+02 - 98ms/epoch - 3ms/step
Epoch 71/100
37/37 - 0s - loss: 2.0427 - r2: -3.9504e+01 - val_loss: 1.2947 - val_r2: -1.6006e+01 - 103ms/epoch - 3ms/step
Epoch 72/100
37/37 - 0s - loss: 1.9840 - r2: -2.9199e+01 - val_loss: 1.8605 - val_r2: -2.6065e+01 - 89ms/epoch - 2ms/step
Epoch 73/100
37/37 - 0s - loss: 1.5932 - r2: -2.1612e+01 - val_loss: 0.7795 - val_r2: -4.4089e+00 - 112ms/epoch - 3ms/step
Epoch 74/100
37/37 - 0s - loss: 0.9020 - r2: -7.0551e+00 - val_loss: 1.1074 - val_r2: -1.0495e+01 - 101ms/epoch - 3ms/step
Epoch 75/100
37/37 - 0s - loss: 1.6549 - r2: -2.2337e+01 - val_loss: 2.6251 - val_r2: -6.0258e+01 - 87ms/epoch - 2ms/step
Epoch 76/100
37/37 - 0s - loss: 1.8053 - r2: -2.4148e+01 - val_loss: 0.6991 - val_r2: -3.4947e+00 - 97ms/epoch - 3ms/step
Epoch 77/100
37/37 - 0s - loss: 0.4749 - r2: -1.4444e+00 - val_loss: 0.3029 - val_r2: -2.2312e-01 - 100ms/epoch - 3ms/step
Epoch 78/100
37/37 - 0s - loss: 1.6607 - r2: -3.2724e+01 - val_loss: 1.8265 - val_r2: -2.5518e+01 - 89ms/epoch - 2ms/step
Epoch 79/100
37/37 - 0s - loss: 1.8024 - r2: -2.3904e+01 - val_loss: 1.3188 - val_r2: -1.3966e+01 - 107ms/epoch - 3ms/step
Epoch 80/100
37/37 - 0s - loss: 1.7573 - r2: -2.3475e+01 - val_loss: 1.4821 - val_r2: -1.8535e+01 - 103ms/epoch - 3ms/step
Epoch 81/100
37/37 - 0s - loss: 0.7507 - r2: -5.6058e+00 - val_loss: 1.9124 - val_r2: -2.8546e+01 - 145ms/epoch - 4ms/step
Epoch 82/100
37/37 - 0s - loss: 1.6884 - r2: -2.4972e+01 - val_loss: 1.1737 - val_r2: -1.0721e+01 - 103ms/epoch - 3ms/step
Epoch 83/100
37/37 - 0s - loss: 1.0647 - r2: -9.6770e+00 - val_loss: 0.7616 - val_r2: -4.0469e+00 - 95ms/epoch - 3ms/step
Epoch 84/100
37/37 - 0s - loss: 1.0574 - r2: -1.1000e+01 - val_loss: 0.8248 - val_r2: -5.1673e+00 - 105ms/epoch - 3ms/step
Epoch 85/100
37/37 - 0s - loss: 0.7202 - r2: -3.8570e+00 - val_loss: 0.5093 - val_r2: -1.4731e+00 - 97ms/epoch - 3ms/step
Epoch 86/100
37/37 - 0s - loss: 0.4883 - r2: -1.4399e+00 - val_loss: 0.2306 - val_r2: 0.2919 - 94ms/epoch - 3ms/step
Epoch 87/100
37/37 - 0s - loss: 0.8617 - r2: -6.5702e+00 - val_loss: 0.8411 - val_r2: -5.0890e+00 - 120ms/epoch - 3ms/step
Epoch 88/100
37/37 - 0s - loss: 0.8168 - r2: -5.6598e+00 - val_loss: 0.3909 - val_r2: -5.2546e-01 - 97ms/epoch - 3ms/step
Epoch 89/100
37/37 - 0s - loss: 0.8954 - r2: -8.4589e+00 - val_loss: 0.2313 - val_r2: 0.2991 - 92ms/epoch - 2ms/step
Epoch 90/100
37/37 - 0s - loss: 1.0023 - r2: -1.0657e+01 - val_loss: 0.5441 - val_r2: -1.7904e+00 - 96ms/epoch - 3ms/step
Epoch 91/100
37/37 - 0s - loss: 1.4418 - r2: -2.1687e+01 - val_loss: 0.6540 - val_r2: -3.1818e+00 - 95ms/epoch - 3ms/step
Epoch 92/100
37/37 - 0s - loss: 0.7682 - r2: -4.4304e+00 - val_loss: 0.2251 - val_r2: 0.3094 - 106ms/epoch - 3ms/step
Epoch 93/100
37/37 - 0s - loss: 1.3607 - r2: -1.6994e+01 - val_loss: 2.7258 - val_r2: -5.7816e+01 - 102ms/epoch - 3ms/step
Epoch 94/100
37/37 - 0s - loss: 1.3640 - r2: -1.3528e+01 - val_loss: 0.6044 - val_r2: -2.2312e+00 - 99ms/epoch - 3ms/step
Epoch 95/100
37/37 - 0s - loss: 0.7606 - r2: -3.8687e+00 - val_loss: 0.2246 - val_r2: 0.3846 - 92ms/epoch - 2ms/step
Epoch 96/100
37/37 - 0s - loss: 0.3448 - r2: -3.8454e-01 - val_loss: 0.4768 - val_r2: -1.1067e+00 - 108ms/epoch - 3ms/step
Epoch 97/100
37/37 - 0s - loss: 0.7749 - r2: -4.2406e+00 - val_loss: 1.2655 - val_r2: -1.2995e+01 - 101ms/epoch - 3ms/step
Epoch 98/100
37/37 - 0s - loss: 0.7480 - r2: -4.3048e+00 - val_loss: 0.4267 - val_r2: -7.8728e-01 - 103ms/epoch - 3ms/step
Epoch 99/100
37/37 - 0s - loss: 0.7482 - r2: -4.1338e+00 - val_loss: 0.3397 - val_r2: -1.6639e-01 - 107ms/epoch - 3ms/step
Epoch 100/100
37/37 - 0s - loss: 1.0969 - r2: -1.3773e+01 - val_loss: 1.4094 - val_r2: -1.4818e+01 - 96ms/epoch - 3ms/step
Model: "sequential_3"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 normalization_3 (Normalizat  (None, 288)              577       
 ion)                                                            
                                                                 
 dense_5 (Dense)             (None, 100)               28900     
                                                                 
 dense_6 (Dense)             (None, 100)               10100     
                                                                 
 dense_7 (Dense)             (None, 1)                 101       
                                                                 
=================================================================
Total params: 39,678
Trainable params: 39,101
Non-trainable params: 577
_________________________________________________________________

from sklearn import metrics as skmetrics

deep_r2_train=skmetrics.r2_score(y_train, y_pred_train_alt)
deep_r2_train

-12.321797441875196